- 시계열 데이터 분석 이해(ARIMA, Prophet 회귀분석 등)

시계열 데이터는 시간 순서대로 정렬된 데이터 포인트의 집합이다. 따라서 시간을 독립변수로 두어 종속변수를 예측을 진행한다. 일반적으로 데이터는 일정한 시간 간격으로 측정된다.

즉, 일정한 시간 간격으로 측정한 데이터이므로 과거 데이터와 현제 데이터 샘플간의 관계가 독립이 아닐 가능성이 높다. 이러한 시계열 데이터의 특징은 다음과 같다.

•

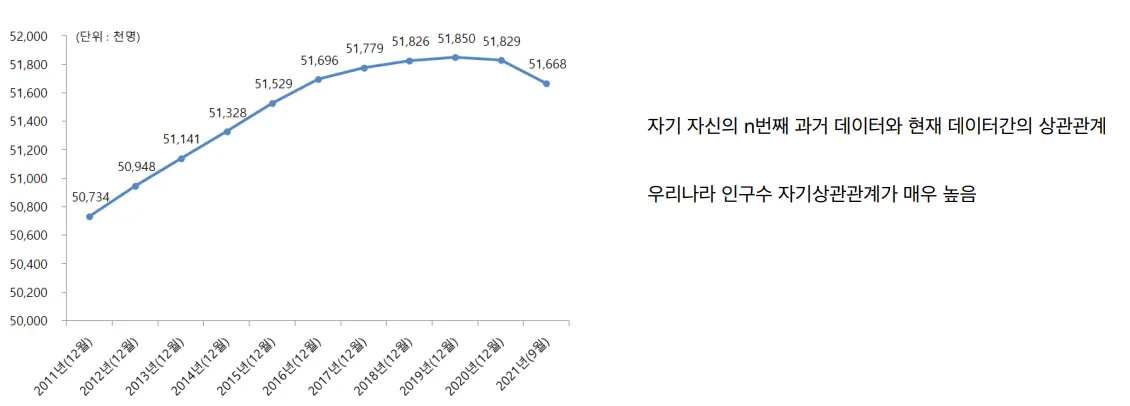
자기 상관관계(Auto Correlation): 시계열 데이터는 시간의 흐름에 따라 서로 상관관계를 가질 수 있으며, 이전의 데이터가 이후 데이터에 영향을 미칠 수 있다.

•

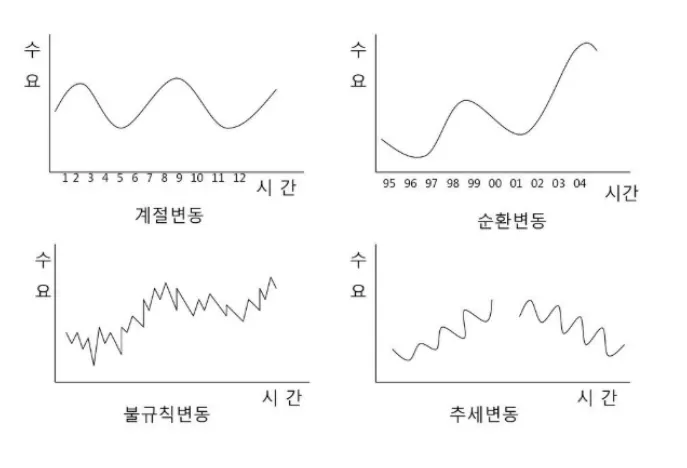
계절성(Seasonality): 일부 시계열 데이터는 특정 시간 주기에 따라 반복되는 패턴을 보일 수 있다. 예를 들어, 매년 특정 시즌에 판매량이 증가하는 소매업의 경우 계절성이 있을 수 있다.

•

추세(Trend): 시계열 데이터는 장기적으로 증가하거나 감소하는 경향을 보일 수 있다.

•

불확실성(Uncertainty): 시계열 데이터의 특성상, 시간의 흐름에 따라 데이터가 어떻게 변할지 예측하는 것은 여러 복잡한 요인에 의해 영향을 받을 수 있으며, 이러한 요인들이 불확실성을 가져온다. 따라서 이에 대한 정량적인 평가가 필요하다.

자기 상관관계를 나타내는 통계량이다. k-시차 만큼 떨어진 데이터 간 상관관계를 측정하여 시계열 데이터의 상관성을 측정한다. 즉, ACF의 절대값이 클 수록 데이터의 상관성이 크다고 볼 수 있다.

ACF(k) = \frac{Cov(y_t,y_{t+k})}{Var(y_t)}

y의 시점과 특정 t-k의 시점 이외의 모든 시점과의 영향력을 배제한 순수한 영향력 나타내는 척도로 시차가 다른 서로 다른 두 데이터 간의 관계만 측정한다.

즉,

y_t

와

y_{t-k}

간의 순수한 상관관계를 계산하기에

y_{t-1},...,y_{t-k+1}

의 영향은 베재한다.

즉,

PACF(k)

는

e_t = y_t - (\beta_1y_{t-1} + ... + \beta_{k-1}\beta_{t-(k-1)})

을 정의하여 다음과 같이 계산한다.

PACF(k) = Corr(e_t, e_{t-k})

모든 시점에 대해서 일정한 평균을 갖도록 하는 것, 즉 추세나 계절성이 없는 시계열 데이터로 만들어 주는 것이다. 정상성을 나타내지 않는 시계열 데이터를 정상 시계열 데이터로 변환하는 방법에는 로그변환과 차분등이 있다.

자기 상관성을 반영하여 이전 관측값이 이후에 영향을 미칠것이라는 아이디어에 기반한 모델이다. AR(p)는 t-시점의 관측값을 이전 p-시차 동안의 선형결합으로 나타낸다.

관측값 이전 시점의 연속적인 예측 오차의 영향을 이용하는 방법이다. 즉,

MA(q): y_t = c + \theta_1\epsilon_{t-1} + ... + \theta_q\epsilon_{t-q} + \epsilon_t

ARIMA(p,d,q)

는 d차 차분한 데이터에

AR(p), MA(q)

모형을 합친 모형이다. 즉, d차 차분한 관측값

y'

에 대해 다음과 같이 나타낸다.

y'_t = c + a_1y'_{t-1} + ... + a_py'_{t-p} + \theta_1\epsilon_{t-1} + \theta_q\epsilon_{t-q} + \epsilon_t