home
History
/////
home
BDA 연혁
ABOUT BDA
BDA TEAM
Class
Content
Mentoring
정규 학회원
일반 학회원
학회 참여 방법
Tech
Report
Newsletter
FAQ
Notice
Review
home
/////

- 선형회귀분석 (2)

기하학적으로 OLS 이해하기

저번 시간에 유도한 OLS estimator를 다른 방법으로 다시 유도해보자. 먼저 우리의 데이터셋이 NN개의 데이터와 pp개의 피쳐들로 이뤄졌다고 하자. 이 때 한개의 데이는 pp개의 피쳐를 갖고 있으므로 벡터로 나타낼 수 있다. 이를 행벡터로 나타내 NN개의 데이터셋을 행렬로 나타내면 N×pN \times p 행렬로 나타낼 수 있다. 여기에 절편을 추가하기 위해 원소가 1인 NN차원 컬럼벡터 j\mathbf{j}를 추가하여 다음과 같이 나타내보자.
X=(j,x1,x2,...xp)∈RN×(p+1)\mathbf{X} = ( \mathbf{j}, \mathbf{x}_1, \mathbf{x_2} , ... \mathbf{x}_p) \in \mathbb{R}^{N \times (p+1)}
구할 회귀계수 β\beta도 벡터로 나타내서 y\mathbf{y}와의 선형 방정식을 행렬표현으로 p+1p+1차원 벡터이고 수식으로 나타내면 아래와 같다.
y=(y1,y2,...yN)T, β=(β0,β1,...,βp)T∈Rp+1\mathbf{y} = (y_1, y_2 , ... y_N)^T, \ \beta = (\beta_0, \beta_1,...,\beta_p)^T \in \mathbb{R}^{p+1}
yi=β0+∑j=1pβjxij+ϵiy=Xβ=β0j+β1x1+β2x2+...+βpxp+ϵ\begin{align*} y_i &= \beta_0 + \sum_{j=1}^p \beta_jx_{ij} + \epsilon_i \\ \mathbf{y} &= \mathbf{X}\beta = \beta_0\mathbf{j} +\beta_1\mathbf{x}_1 + \beta_2\mathbf{x}_2+ ... + \beta_p\mathbf{x}_p + \mathbf{\epsilon} \end{align*}
ϵ=(ϵ1,...,ϵN)T\mathbf{\epsilon} = (\epsilon_1,...,\epsilon_N)^T는 오차로 관측되지 않는 확률변수이다. 편의를 위해 기댓값이 0이고 분산이 σ2\sigma^2인 i.i.d 가정을 하겠다.
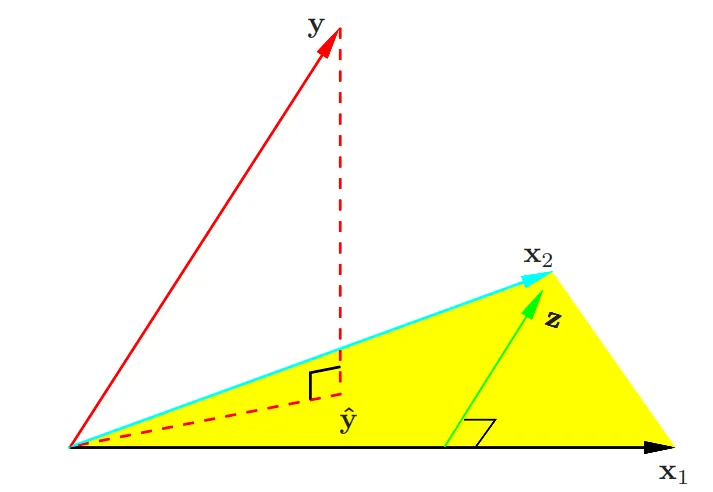
즉, 예측값은 X\mathbf{X}의 열벡터의 선형결합으로 표현이 가능하고, 따라서 X의 열공간상의 벡터이다. OLS는 실제값과 예측값의 차이인 잔차의 제곱합을 최소화하는 것이 목표이다. 자세한 증명은 생략하겠지만, 직관적으로 이러한 잔차가 X\mathbf{X}의 열공간과 수직을 이룰때에가 잔차가 가장 작음을 알 수 있다. 따라서 y\mathbf{y}를 X\mathbf{X}의 열공간에 정사영시킨 벡터가 OLS의 예측값이다.
두 벡터가 수직이면 내적값은 0이라는 것을 우리는 알고 있다. 따라서 잔차는 X\mathbf{X}의 열공간의 모든 벡터와 수직이여야 한다. 수식으로 나타내면 다음과 같다.
0=⟨Xβ,y−y^⟩=⟨Xβ,y−Xβ^⟩ for all β∈Rp 0=\left\langle \mathbf{X}\beta , \mathbf{y} - \hat{\mathbf{y}}\right\rangle = \left\langle \mathbf{X}\beta , \mathbf{y} - \mathbf{X}\hat{\beta}\right\rangle \ \text{for all} \ \beta \in \mathbb{R}^p
0=⟨Xβ,y−Xβ^⟩ =(Xβ)T(y−Xβ^)=βTXT(y−Xβ^)  for all β∈Rp∴XT(y−Xβ^)=0 \begin{align*} 0 &= \left\langle \mathbf{X}\beta, \mathbf{y} - \mathbf{X}\hat{\beta} \right\rangle \ = (\mathbf{X}\beta)^T(\mathbf{y} - \mathbf{X}\hat{\beta}) \\ &= \beta^T\mathbf{X}^T(\mathbf{y} - \mathbf{X}\hat{\beta}) \ \text{ for all } \beta \in\mathbb{R}^p\end{align*} \\ \therefore \mathbf{X}^T(\mathbf{y} - \mathbf{X}\hat{\beta}) = 0
따라서 최적해는 위 방정식을 풀면 유도된다.
XTXβ^=XTyβ^=(XTX)−1XTy\begin{align*} \mathbf{X}^T\mathbf{X}\hat{\beta} &= \mathbf{X}^T\mathbf{y} \\ \hat{\beta} &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \end{align*}
H=X(XTX)−1XT\mathbf{H} = \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T는 hat matrix라고 불리며, 벡터 y\mathbf{y}를 X\mathbf{X}의 열공간에 정사영시키는 행렬이다.
y^=Xβ=X(XTX)−1XTy=Hy\hat{\mathbf{y}} = \mathbf{X}\beta = \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} = \mathbf{H}\mathbf{y}

통계적 추론

β^\hat{\beta}의 기댓값과 분산을 계산해보자.
E(β^)=(XTX)−1XTE(y)=(XTX)−1XTXβ=βVar(β^)=(XTX)−1XTVar(β)((XTX)−1XT)T=σ2(XTX)−1\begin{align*} \mathbb{E}(\hat{\beta}) &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbb{E}(\mathbf{y} ) = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T \mathbf{X}\beta = \beta \\ Var(\hat{\beta}) &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^TVar(\beta)((\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T)^T = \sigma^2(\mathbf{X}^T\mathbf{X})^{-1} \end{align*}
보통 오차항의 분산 σ2\sigma^2는 알 수 없으므로, 다음과 같은 추정량을 사용한다.
σ^2=1N−p−1∥y−Xβ^∥2=1N−p−1yT(I−H)y\hat{\sigma}^2 = \frac{1}{N-p-1}\|\mathbf{y} - \mathbf{X}\hat{\beta} \|^2 = \frac{1}{N-p-1}\mathbf{y}^T(\mathbf{I}-\mathbf{H})\mathbf{y}
Note. II를 N×NN \times N 항등행렬이라 할때, 위 추정량은 불편추정량임을 다음과 같이 보일 수 있다.
E(σ^2)=1N−p−1E(tr(yT(I−H)y) (∵yT(I−H)y∈R)=1N−p−1E(tr((I−H)yyT)=1N−p−1tr((I−H)E(yyT)=1N−p−1tr((I−H)Var(y))=1N−p−1tr((I−H)σ2)=1N−p−1(N−p−1)σ2=σ2\begin{align*} \mathbb{E}(\hat{\sigma}^2) &= \frac{1}{N-p-1}\mathbb{E}(tr(\mathbf{y}^T(\mathbf{I} - \mathbf{H})\mathbf{y}) \ (\because \mathbf{y}^T(\mathbf{I} - \mathbf{H})\mathbf{y} \in \mathbb{R}) \\ &= \frac{1}{N-p-1}\mathbb{E}(tr((\mathbf{I} - \mathbf{H})\mathbf{y}\mathbf{y}^T) \\ &= \frac{1}{N-p-1}tr((\mathbf{I} - \mathbf{H})\mathbb{E}(\mathbf{y}\mathbf{y}^T) \\ &= \frac{1}{N-p-1}tr((\mathbf{I} - \mathbf{H})Var(\mathbf{y})) \\ &= \frac{1}{N-p-1}tr((\mathbf{I} - \mathbf{H})\sigma^2) = \frac{1}{N-p-1}(N-p-1)\sigma^2 = \sigma^2 \end{align*}
추가적으로 오차항이 정규분포를 따른다고 가정하면, 다음이 성립한다.
β^∼N(β,(XTX)−1σ2)(N−p−1)σ2∼σ2χ2(N−p−1)\begin{align*} \hat{\beta} &\sim \mathcal{N}(\beta, (\mathbf{X}^T\mathbf{X})^{-1}\sigma^2) \\ (N-p-1)\sigma^2 &\sim \sigma^2\chi^2(N-p-1) \end{align*}
회귀계수에 대한 가설 검정은 βj=0\beta_j = 0에 대한 귀무가설을 통해 검정하며 아래와 같은 z-점수를 사용한다.
zj=β^jσ^vjz_j = \frac{\hat{\beta}_j}{\hat{\sigma}\sqrt{v_j}}
vjv_j는 (XTX)−1(\mathbf{X}^T \mathbf{X})^{-1}의 jj번째 대각원소이다. 귀무가설 하에서 zjz_j는 자유도가 (N−p−1)(N-p-1)인 t-분포를 따른다. 충분히 큰 NN에 대해서는 정규분포와 큰 차이가 없기에 정규분포를 사용하여도 된다. 즉, 정규분포를 생각해보면 zjz_j가 큰 값을 가진다는 것은 귀무가설을 기각할 수 있기에 의미 있는 회귀계수라고 볼 수 있다.
또한 (1−2α)(1-2\alpha) 신뢰구간은 (β^j−z(1−α)vjσ^,β^j+z(1−α)vjσ^)(\hat{\beta}_j - z^{(1-\alpha)}\sqrt{v_j}\hat{\sigma}, \hat{\beta}_j + z^{(1-\alpha)}\sqrt{v_j}\hat{\sigma} )이다.
만약 βj\beta_j의 조합간의 모델 차이를 보고 싶다면 다음과 같은 F-통계량을 사용한다.
F=(RSS0−RSS1)(p1−p0)RSS1/(N−p1−1)F = \frac{(RSS_0 - RSS_1)(p_1 - p_0)}{RSS_1/(N-p_1-1)}
RSS1RSS_1은 (p1+1)(p_1+1)개의 파라미터를 가진 모델의 잔차제곱합이고, RSS0RSS_0는 이보다 작은, 첫번째 모델에 포함되는 p0+1p_0+1개의 파라미터를 가진 모델의 잔차제곱합이다. 만약 더 작은 모델이 맞다면, 즉 나머지 (p1−p0)(p_1 - p_0)개의 회귀계수가 0이었다면 이는 Fp1−p0,N−p1−1F_{p_1-p_0, N-p_1-1}분포를 따른다. 마찬가지로 충분히 큰 NN에 대해서 χ2(p1−p0)\chi^2(p_1-p_0)을 따른다.