home
History
/////
home
BDA 연혁
ABOUT BDA
BDA TEAM
Class
Content
Mentoring
정규 학회원
일반 학회원
학회 참여 방법
Tech
Report
Newsletter
FAQ
Notice
Review
home
/////

- DBSCAN, GMM 등 다양한 클러스터링 예시

EM(Expectation-Maximization) 알고리즘이란?

p(x,z∣θ)p(\mathbf{x}, \mathbf{z}|\theta)가 주어졌을 때 EM 알고리즘은 다음과 같이 작동한다.
1.
θ(0)\theta^{(0)}을 초기화한다.
2.
(E-step) p(z∣x,θ(n))p(\mathbf{z}|\mathbf{x},\theta^{(n)})를 계산한다.
3.
(M-step) Q(θ,θ(n))=∑zp(z∣x,θ(n))log⁡p(x,z∣θ)Q(\theta, \theta^{(n)}) = \sum_{\mathbf{z}} p(\mathbf{z}|\mathbf{x}, \theta^{(n)})\log{p(\mathbf{x},\mathbf{z}|\theta)}를 정의하고 θ(n+1):=arg max⁡θQ(θ,θ(n))\theta^{(n+1)} := \argmax_{\theta} Q(\theta, \theta^{(n)})으로 업데이트를 진행한다.
z\mathbf{z}에 대한 임의로 확률분포 qq를 정의하면 로그가능도 l(θ):=log⁡p(x∣θ)=log⁡∑zp(x,z∣θ)l(\theta) := \log{p(\mathbf{x}|\theta)} = \log \sum_{\mathbf{z}}p(\mathbf{x},\mathbf{z} |\theta)는 다음과 같은 부등식을 따른다.
l(θ)=log⁡∑zp(x,z∣θ)=log⁡∑zq(z)p(x,z∣θ)q(z)≥∑zq(z)log⁡p(x,z∣θ)q(z)=L(q,θ)\begin{align*} l(\theta) &= \log \sum_{\mathbf{z}}p(\mathbf{x},\mathbf{z} |\theta) \\ &= \log{\sum_{\mathbf{z}} q(\mathbf{z})\frac{p(\mathbf{x},\mathbf{z}|\theta)}{q(\mathbf{z})}} \\ &\geq \sum_{\mathbf{z}}q(\mathbf{z})\log{\frac{p(\mathbf{x},\mathbf{z}|\theta)}{q(\mathbf{z})}} \\ &= \mathcal{L}(q,\theta) \end{align*}
이는 로그 함수가 단조증가함수라는 사실과 옌센 부등식(Jensen's inequality)을 통해 유도되었다. EM 알고리즘의 목표는 q,θq,\theta를 통해 로그 가능도의 하한인 L(q,θ)\mathcal{L}(q,\theta)를 최대화하는 것이다.
먼저 베이즈 정리에 의해 p(x,z∣θ)=p(z∣x,θ)p(x∣θ)p(\mathbf{x},\mathbf{z}|\theta) = p(\mathbf{z}|\mathbf{x},\theta) p(\mathbf{x}|\theta) 이다. 이를 이용하여 L(q,θ)\mathcal{L}(q,\theta)를 다음과 같이 분해해보자.
L(q,θ)=∑zq(z)log⁡p(x,z∣θ)q(z)=∑zq(z)log⁡p(z∣x,θ)q(z)+∑zq(z)log⁡p(x∣θ)=∑zq(z)log⁡p(z∣x,θ)q(z)+log⁡p(x∣θ)=∑zq(z)log⁡p(z∣x,θ)q(z)+l(θ)\begin{align*} \mathcal{L}(q,\theta) &= \sum_{\mathbf{z}}q(\mathbf{z})\log{\frac{p(\mathbf{x},\mathbf{z}|\theta)}{q(\mathbf{z})}} = \sum_{\mathbf{z}}q(\mathbf{z})\log{\frac{p(\mathbf{z}|\mathbf{x}, \theta)}{q(\mathbf{z})}} + \sum_{\mathbf{z}}q(\mathbf{z}) \log{p(\mathbf{x}|\theta)} \\ &= \sum_{\mathbf{z}}q(\mathbf{z})\log{\frac{p(\mathbf{z}|\mathbf{x}, \theta)}{q(\mathbf{z})}} + \log{p(\mathbf{x}|\theta)} = \sum_{\mathbf{z}}q(\mathbf{z})\log{\frac{p(\mathbf{z}|\mathbf{x}, \theta)}{q(\mathbf{z})}} + l(\theta) \end{align*}
위 식의 첫번째 항은 ∑iqilog⁡piqi\sum_i q_i \log{\frac{p_i}{q_i}}꼴로, 마찬가지로 다음과 같이 옌센 부등식을 이용하여 0보다 작거나 같음을 알 수 있다.
∑iqilog⁡qipi≤log⁡∑iqipiqi=0\sum_i q_i \log{\frac{q_i}{p_i}} \leq \log{\sum_i q_i\frac{p_i}{q_i}} = 0
(등식은 p=qp=q일때 성립함을 알 수 있다.)
이를 쿨백-라이블러 발산(Kullback–Leibler divergence)이라고하며, 다음과 같이 표기한다.
∑zq(z)log⁡p(z∣x,θ)q(z)=−DKL(q(z)∣∣p(z∣x,θ))\sum_{\mathbf{z}}q(\mathbf{z})\log{\frac{p(\mathbf{z}|\mathbf{x}, \theta)}{q(\mathbf{z})}} = -\mathbb{D}_{KL}(q(\mathbf{z})|| p(\mathbf{z}|\mathbf{x}, \theta))
Q2. 이는 이전시간에 결정트리에서 배운 엔트로피와 비슷해보인다. 쿨백-라이블러 발산에 대해서 찾아보자.
다시 정리해보자면, L(q,θ)=−DKL(q(z)∣∣p(z∣x,θ))+l(θ)\mathcal{L}(q,\theta) = -\mathbb{D}_{KL}(q(\mathbf{z})|| p(\mathbf{z}|\mathbf{x}, \theta)) + l(\theta) 이고, L(q,θ)\mathcal{L}(q,\theta)를 최대화 해야하므로, 이는 −DKL(q(z)∣∣p(z∣x,θ))-\mathbb{D}_{KL}(q(\mathbf{z})|| p(\mathbf{z}|\mathbf{x}, \theta))가 0이 될 경우이기에 따라서 q(z)=p(z∣x,θ)q(\mathbf{z}) = p(\mathbf{z}|\mathbf{x},\theta) 일 때 최대가 된다.
위의 E-step과 M-step이 어떻게 유도되었는지는 다음과 같다.
정리
E-step: θ\theta를 고정하여 로그가능도의 하한의 최대를 계산한다. 즉, 매 단계마다 θ=θ(n)\theta = \theta^{(n)}로 둔다.
qn=arg max⁡qL(q,θ(n))=−DKL(q(z)∣∣p(z∣x,θ(n)))+l(θ(n))=p(z∣x,θ(n))q_n = \argmax_{q} \mathcal{L}(q,\theta^{(n)}) = -\mathbb{D}_{KL}(q(\mathbf{z})|| p(\mathbf{z}|\mathbf{x}, \theta^{(n)})) + l(\theta^{(n)}) = p(\mathbf{z}|\mathbf{x},\theta^{(n)})
M-step: q=qnq = q_n으로 고정하여 최대가 되도록 하는 θ\theta를 계산하여 θ(n+1)\theta^{(n+1)}를 업데이트한다.
θ(n+1)=arg max⁡θL(qn,θ)=arg max⁡θ∑zqn(z)log⁡p(x,z∣θ)−∑zqn(z)log⁡qn(z)=arg max⁡θ∑zp(z∣x,θ(n))log⁡p(x,z∣θ)=arg max⁡θQ(θ,θ(n))\begin{align*} \theta^{(n+1)} &= \argmax_{\theta} \mathcal{L}(q_n,\theta) \\ &= \argmax_{\theta} \sum_{\mathbf{z}} q_n(\mathbf{z})\log{p(\mathbf{x},\mathbf{z}|\theta)}- \sum_{\mathbf{z}}q_n(\mathbf{z})\log{q_n(\mathbf{z})} \\ &= \argmax_{\theta} \sum_{\mathbf{z}}p(\mathbf{z}|\mathbf{x},\theta^{(n)})\log{p(\mathbf{x},\mathbf{z}|\theta)} \\ &= \argmax_{\theta} Q(\theta, \theta^{(n)}) \end{align*}
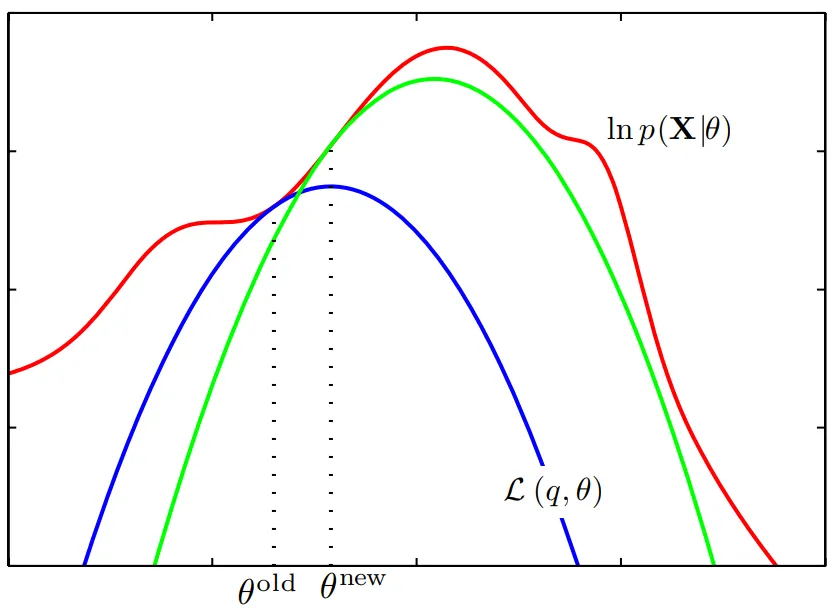
θ(old)\theta^{(old)}에서의 L(q,θ)\mathcal{L}(q,\theta)를 구해서(파란색 함수, 현재 단계에서 로그가능도의 ln⁡p(X∣θ)\ln p(\mathbf{X}|\theta)의 하한) 이를 최대화 하는 θ(new)\theta^{(new)}를 Q(θ,θ(old))Q(\theta, \theta^{(old)})를 통해 구한다. 마찬가지로 θ(new)\theta^{(new)}에서 로그 가능도의 하한(녹색 함수)을 구해 이를최대화하도록 θ\theta를 업데이트하여 둘의 차이가 없을 때 까지 반복한다.

EM알고리즘으로 GMM 구현하기