Density-Based Spatial Clustering of Applications with Noise(DBSCAN)이란?
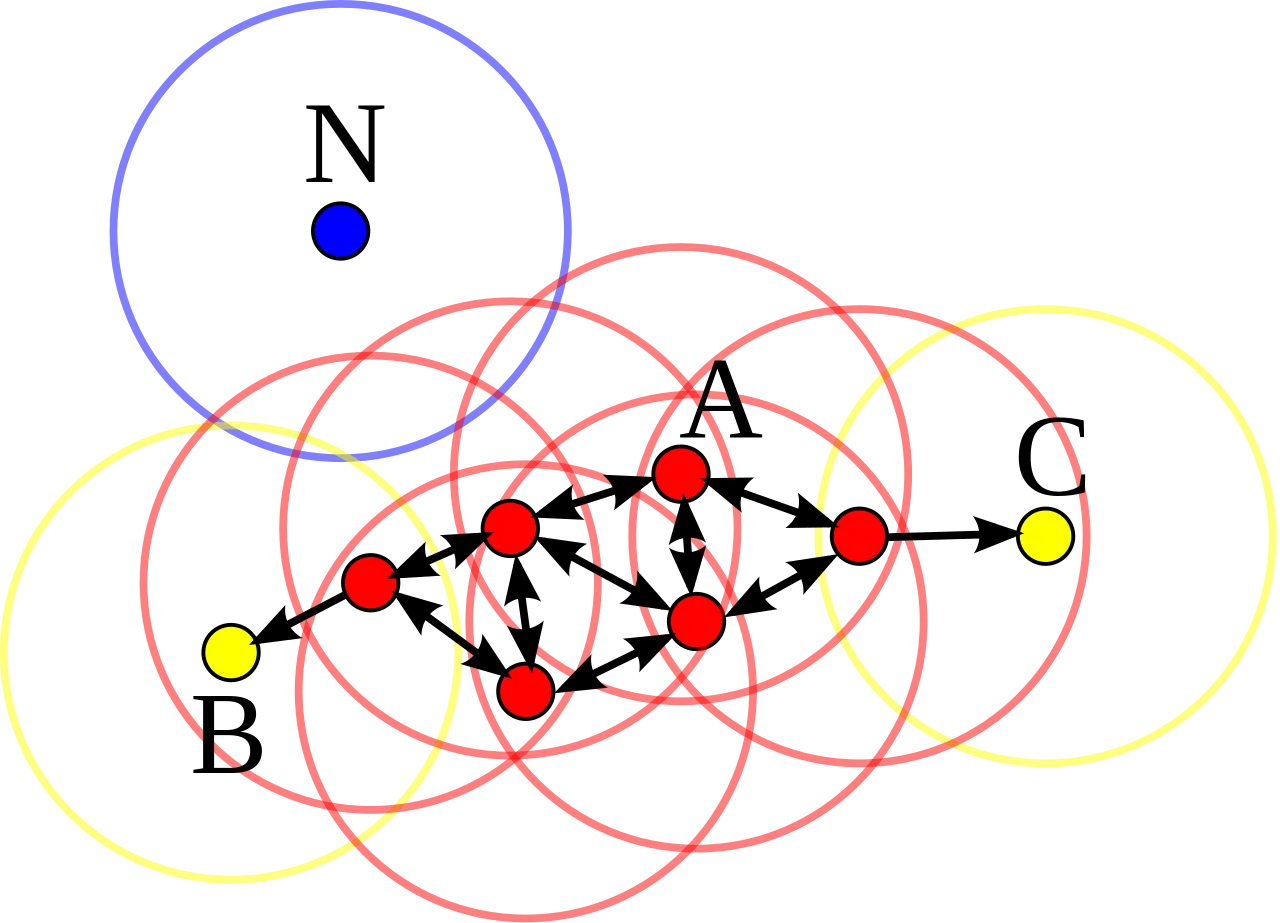
DBSCAN은 연속적으로 밀집된 샘플들을 클러스터로 정의한다. 각 샘플마다 반경내에 놓여있는 샘플 수를 세어 min_samples 보다 크거나 같으면 핵심샘플(core point) 이라고 간주하고, min_samples수보다 적지만 반경 내에 핵심샘플이 존재하면 경계점 샘플(border point), 이외에는 이상치(noise pint)라고 간주한다. DBSCAN은 연속적으로 반경내에 높인 핵심샘플들의 집합을 하나의 군집으로 간주한다.
아래 그림은 min_samples를 4로, 반경은 샘플 주위의 원으로 표시하였다. 빨간색 점 들은 핵심 샘플, 노란색 점 는 경계점 샘플, 파란색 점 은 이상치로 구별된 것을 확인할 수 있다.
작동과정은 다음과 같다.
1.
모든 샘플마다 반경내에 놓여있는 샘플 수을 세어 적어도 min_samples 개의 샘플이 있다면 핵심 샘플로 간주한다.
2.
핵심 샘플의 반경내에 놓인 샘플들은 모두 하나의 군집으로 간주한다.
3.
핵심 샘플도 아니며 핵심 샘플의 반경내에 놓이지 않은 샘플은 이상치로 간주한다.
DBSCAN의 특징1.
K-Means에서는 군집 수를 조절해나가면서 주관적인 방법으로 적절한 군집 수를 선정하였었다. 하지만 DBSCAN에서는 이러한 과정이 필요가 없다.
2.
K-Menas의 경우 원 모양으로 분포한 데이터셋에서의 군집화가 어려웠지만, DBSCAN의 경우 군집의 모양과 개수에 상관없이 군집화가 가능하다.
3.
이상치(noise point)를 알고리즘 내에서 간주하기 때문에 robust하다.
4.
데이터의 입력 순서가 달라지면 다른 결과를 낼 수 있다.
5.
데이터의 분포를 모를 경우 적절한 와 min_samples을 찾기 어렵다.
Note. 사이킷런에서 제공하는 sklearn.cluster.DBSCAN 클래스에서는 predict()가 아닌, fit_predict()를 제공한다. 즉, K-Means와 다르게 새로운 샘플에 대해서는 예측을 진행하지 못한다. 이는 알고리즘의 작동과정과 관련이 있는데 왜 그런지 생각해보자.