home
History
///
home
BDA 연혁
ABOUT BDA
BDA TEAM
Class
Content
Mentoring
정규 학회원
일반 학회원
학회 참여 방법
Tech
Report
Newsletter
FAQ
Notice
Review
home
///

- 비지도학습 실습 ( DBSCAN, Kaggle 코드 리뷰)

가우시안 혼합 모델(Gaussian Mixture Model, GMM)이란?

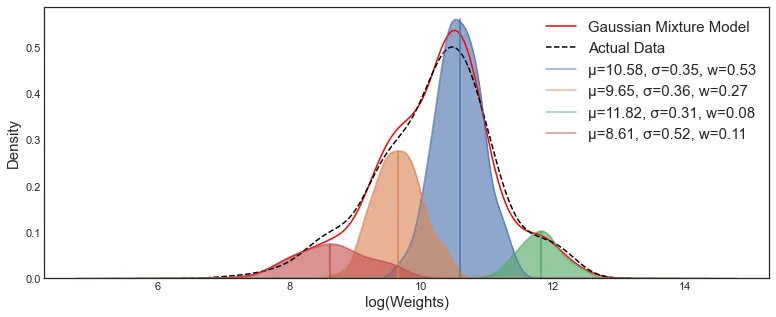
가우시안 혼합모델(GMM)은 샘플이 모수가 알려지지 않은 여러개의 혼합된 가우시안 분포를 따를 것이라는 가정하는 확률모델이다.
가우시안 혼합 분포는 다음과 같이 정의할 수 있다.
p(x)=∑k=1KπkN(x;μk,Σk) where ∑k=1Kπk=1,πk∈[0,1] for all kp(\mathbf{x}) = \sum_{k=1}^{K} \pi_k \mathcal{N}(\mathbf{x};\mu_k, \Sigma_k) \ \text{where} \ \sum_{k=1}^K \pi_k = 1, \pi_k \in [0,1] \ \text{for all} \ k
πk\pi_k는 가우시안 혼합 분포에서 kk번째 가우시안 분포의 비율이다. 즉, GMM은 학습데이터 X=(x1,...,xN)\mathbf{X} = (\mathbf{x}_1, ..., \mathbf{x}_N)를 통해 θ={π1,...πK,μ1,...μK,Σ1,...ΣK}\theta = \{ \pi_1,...\pi_K,\mu_1,...\mu_K, \Sigma_1,...\Sigma_K \}를 추정하는 것이다. MLE를 통해 이를 추정해보자. 위 확률분포의 로그 가능도는 다음과 같다.
L(X∣θ)=∑n=1Nlog⁡(∑k=1KπkN(xn;μk,Σk))\mathcal{L}(\mathbf{X}|\theta) = \sum_{n=1}^N \log(\sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{x}_n; \mu_k,\Sigma_k))
위 식을 각 모수에 대해 편미분을 통해 바로 최적의 해가 유도되지 않는다. 통계학에서는 이를 바로 구하기 힘들때 잠재변수(latent variable)를 두어 추정한다. 유도과정은 다음과 같다.
Q1. 위 로그가능도를 μk\mu_k에 대해 편미분하여 왜 계산이 힘든지 알아보자.
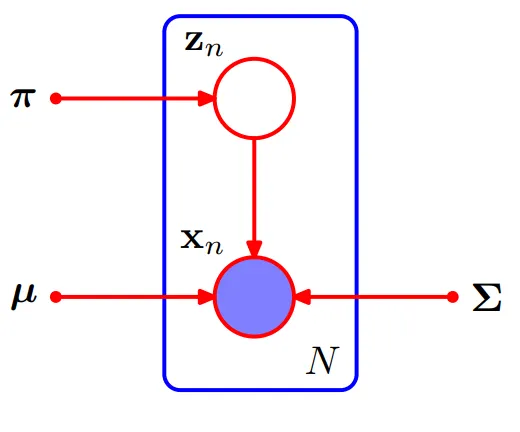
GMM은 학습데이터 X=(x1,...,xN)\mathbf{X} = (\mathbf{x}_1, ..., \mathbf{x}_N)를 다음과 같이 생성되었다고 가정한다.
1.
샘플마다 KK개의 군집에서 랜덤하게 한 군집이 선택된다. kk번째 군집을 선택할 확률은 πk\pi_k로 정의된다. 샘플을위해 선택한 군집 인덱스는 z\mathbf{z}로 표시한다. 각 인덱스 z=(z1,...,zK)∈RK\mathbf{z} = (z_{1}, ..., z_{K}) \in \mathbb{R}^K는 kk번째 군집에 군집에 속한다면, kk번째 원소가 1이고 나머지는 0인 KK차원 컬럼 벡터로 표시할 수 있다. 즉 p(zk=1)=πkp(z_{k} = 1 ) = \pi_k이다. 따라서, p(z)=∏k=1Kπkzkp(\mathbf{z}) = \prod_{k=1}^K \pi_k^{z_k} 이다.
2.
z=k\mathbf{z} = k이면, 즉 샘플 x\mathbf{x}가 kk번째 군집에 할당되었다면, 해당 샘플은 평균이 μk\mu_k이고, 분산이 Σk\Sigma_k인 가우시안 분포에서 랜덤하게 샘플링된 것이다. 다시 말해서 x∼N(μk,Σk)\mathbf{x} \sim \mathcal{N}(\mu_k, \Sigma_k)이다.
위 과정을 그래프 모형으로 나타내면 다음과 같다.
샘플 x\mathbf{x}를 군집 인덱스 z\mathbf{z}에 대한 결합 분포로 나타내면 p(x∣z)=∏k=1KN(x∣μk,Σk)zkp(\mathbf{x} | \mathbf{z}) = \prod_{k=1}^K \mathcal{N}(\mathbf{x} | \mu_k, \Sigma_k)^{z_k}이다. 이 결합확률 분포를 x\mathbf{x}에 대한 주변 확률분포로 나타내면 다음과 같다.
p(x)=∑zp(z)p(x∣z)=∑z∏k=1K(πkN(x∣μk,Σk))zk=∑k=1KπkN(x∣μk,Σk)p(\mathbf{x}) = \sum_{\mathbf{z}} p(\mathbf{z})p(\mathbf{x} | \mathbf{z}) = \sum_{\mathbf{z}} \prod_{k=1}^K (\pi_k\mathcal{N}(\mathbf{x} | \mu_k, \Sigma_k))^{z_k} = \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{x} | \mu_k, \Sigma_k)
즉, p(x)p(\mathbf{x})대신, p(x∣z)p(\mathbf{x} | \mathbf{z})를 통해 로그가능도를 최대화하는 것이 아닌, 로그가능도의 하한을 최대화하는 EM(Expectation-Maximization) 알고리즘을 통해 GMM을 학습한다. EM 알고리즘과 이를 통한 GMM의 학습과정은 다음시간에 알아보자.